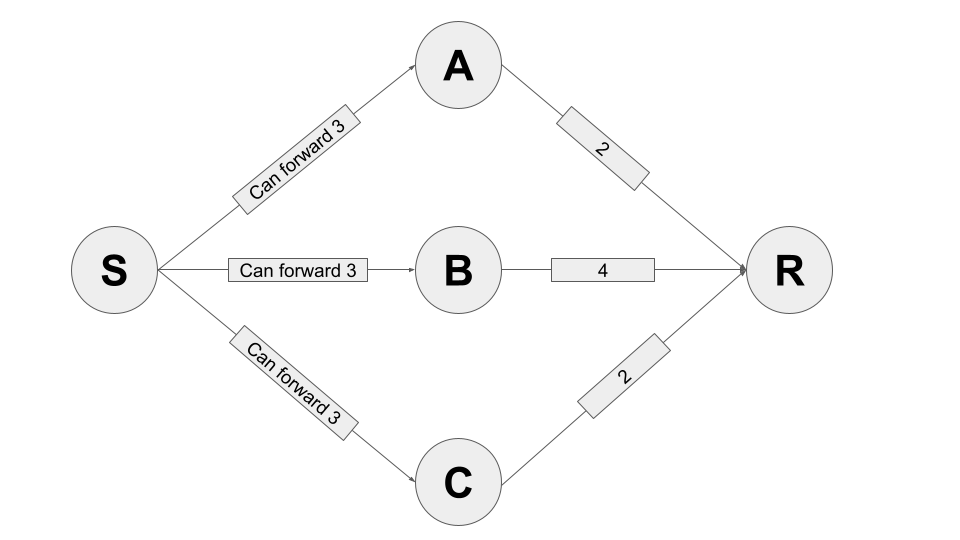
Take a look at the next community instance:
Assume S desires to ship 3 sats to R. You may additional assume that S has sufficient liquidity in every of its native channels to ship as much as 3 sats. Additionally assume the liquidity in channels (A,R), (B,R) and (C,R) is uniformly distributed.
one optimally dependable cost circulate on this diagram seems like this:
1 sat: S --> A --> R likelihood: 2/3
2 sats: S --> B --> R likelihood: 3/5
This circulate has a complete likelihood of 2/3*3/5 = 2/5 = 0.4 = 40%
The query:
How you can compute the anticipated worth of Satoshis to reach at R if S sends 3?
Choice A
(which I already know is mistaken however I write it down as a result of I think some folks might need an identical first thought)
Initially I believed this could simply be 3 sats * 2/5 = 6/5 sats = 1.2 sats which is what one will get from multiplying the quantity to ship with the likelihood of the circulate. This appears unusual as sending 2 sats alongside S-->B-->R has a likelihood of 3/5 and with the reasoning of above an expectation worth of 2 sats * 3/5 = 6/5 sats = 1.2 sats. because the anticipated worth for 1 sat alongside the S-->A-->B path is bigger than 0 this could be a contradiction to the additivity of the anticipated worth.
Choice B
Ranging from the above reasoning we add the anticipated values for the disjoint paths so:
E[3 sats] = 1 sat * 2/3 + 2 sat * 3/5 = 10/15 sats + 18/15 sats = 28/15 sats
Choice C
After all the two satoshi path S-->B-->R doesn’t need to be despatched as one onion however might be despatched as two onions with 1 sat every:
The primary has a likelihood of 4/5 and the second has a conditional likelihood of 3/4 which is extensively defined at this problem. With the logic from choice B one ought to be capable of add these anticipated values.
so we’ve got the anticipated worth for sending two sats in two seperate 1 sat onions alongside S--> B --> R can be computed as:
E[2 sats] = 1 sat * 4/5 + 1 sat * 3/4 = 31/20 sats
If we add the 1 sat onion from the S-->A-->R which was 2/3 sats
we’d count on to have
E[3 sats] = 31/20 sats + 2/3 sats = 93/60 sats + 40/60 sats = 132/60 sats = 33/15 sats
That is 5/15 sats = 1/3 sats greater than the reply in choice B
Choice D
To make issues worse I’m confused if the anticipated values of dissecting the two sat onion in choice C into two 1 sat onions can simply linearly added up because the second onion is conditioned on having 2 sats of liquidity within the channel. If the primary onion has failed the second will definitely fail. Thus one must compute anticipated worth for sending two 1 sat onions like this:
E[2 sats] = 1 sat * 4/5 + 1 sat * 3/5 = 7/5 sats
this could end in a complete anticipated worth of:
E[3 sats] = 2/3 sats + 7/5 sats = 10/30 sats + 21/15 sats = 31/15 sats
Ideas
only for comparability listed below are the outcomes
- Choice A:
18/15 - Choice B:
28/15 - Choice C:
33/15 - Choice D:
31/15
Whereas Choice B appears actually proper it is sensible to additional dissect the two sats onion. In simulations I did plainly Choice D is appropriate which is a bit shocking for me. Utilizing the formalism of likelihood concept the distinction for the two sat path is:
- Choice C:
E[2 sats] = 1 sat * P(X>=1) + 1 sat * P(X>=2 | X >= 1) - Choice D:
E[2 sats] = 1 sat * P(X>=1) + 1 sat * P(X>=2)
As mentioned the simulated setting signifies that Choice D is the right reply however that’s extremely shocking to me as I’d count on the second time period to be a conditional probabilty.